1.Artificial Intelligence vs. Human Intelligence

1.1 How did early artificial intelligence models draw inspiration from our understanding of the brain?

The early development of artificial intelligence was greatly influenced by our understanding of the human brain. In the mid-20th century, advancements in neuroscience and initial insights into brain function led scientists to attempt applying these biological concepts to the development of machine intelligence.

In 1943, neurophysiologist Warren McCulloch and mathematician Walter Pitts introduced the “McCulloch-Pitts neuron model,” one of the earliest attempts in this area. This model described the activity of neurons using mathematical logic, which, although simplistic, has laid the groundwork for later artificial neural networks.

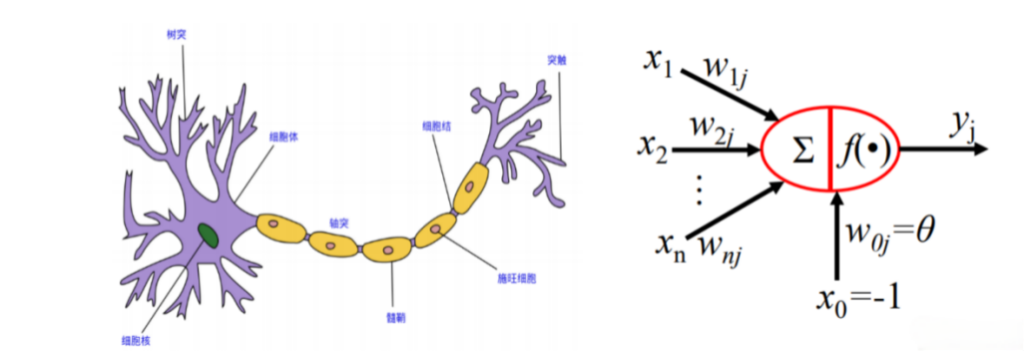
▷ Fig.1: Structure of a neuron and the McCulloch-Pitts neuron model.

During this period, brain research primarily focused on how neurons process information and interact within complex networks via electrical signals. These studies inspired early AI researchers to design primitive artificial neural networks.

In the 1950s, the perceptron, invented by Frank Rosenblatt, was an algorithm inspired by biological visual systems, simulating how the retina processes information by receiving light. Although it was rudimentary, it marked a significant step forward in the field of machine learning.

 

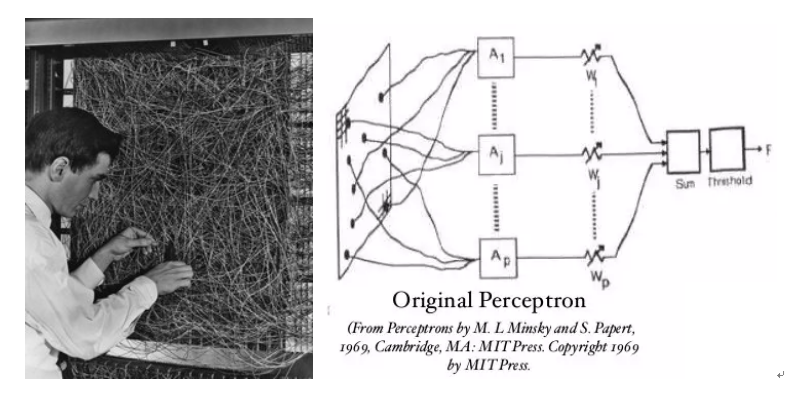▷ Fig.2: Left: Rosenblatt’s physical perceptron; Right: Structure of the perceptron system.

In addition to the influence of neuroscience, early cognitive psychology research also contributed to the development of AI. Cognitive psychologists sought to understand how humans perceive, remember, think, and solve problems, providing a methodological foundation for simulating human intelligent behavior in AI. For instance, the logic theorist developed by Allen Newell and Herbert A. Simon could prove mathematical theorems [1-3], simulating the human problem-solving process and, to some extent, mimicking the logical reasoning involved in human thought.

Although these early models were simple, their development and design were profoundly shaped by contemporary understandings of the brain, which established a theoretical and practical foundation for the development of more complex systems. Through such explorations, scientists gradually built intelligent systems capable of mimicking or even surpassing human performance in specific tasks, driving the evolution and innovation of artificial intelligence technology.

1.2 Development of Artificial Intelligence

Since then, the field of artificial intelligence has experienced cycles of “winters” and “revivals.” In the 1970s and 1980s, improvements in computational power and innovations in algorithms, such as the introduction of the backpropagation algorithm, made it possible to train deeper neural networks. During this period, although artificial intelligence achieved commercial success in certain areas, such as expert systems, limitations that arose from technology and overly high expectations ultimately led to the first AI winter.

Entering the 21st century, especially after 2010, the field of artificial intelligence has witnessed unprecedented advancements. The exponential growth of data, the proliferation of high-performance computing resources like GPUs, and further optimization of algorithms propelled deep learning technologies as the main driving force behind AI development.

The core of deep learning remains the simulation of how brain neurons process information, and its applications have far surpassed initial expectations, encompassing numerous fields such as image recognition, natural language processing, autonomous vehicles, and medical diagnostics. These groundbreaking advancements have not only driven technological progress but also fostered the emergence of new business models and rapid industry development.

▷ Giordano Poloni

1.3 Differences Between Artificial Intelligence and Human Intelligence

1.3.1 Differences in Functional Performance

Although artificial intelligence has surpassed human capabilities in specific domains such as board games and certain image and speech recognition tasks, it generally lacks cross-domain adaptability. While some AI systems, particularly deep learning models, excel in big data environments, they typically require vast amounts of labeled data for training, and their transfer learning abilities are limited when tasks or environments change, often necessitating the design of specific algorithms. In contrast, the human brain possesses a robust learning and adaptation capacity, which is able to learn new tasks with minimal data across various conditions and perform transfer learning, applying knowledge gained in one domain to seemingly unrelated areas.

In terms of flexibility in addressing complex problems, AI performs best with well-defined and structured issues, such as board games and language translation. However, its efficiency drops when dealing with ambiguous and unstructured problems, which makes it susceptible to interference. The human brain exhibited high flexibility and efficiency in processing vague and complex environmental information; for instance, it can recognize sounds in noisy environments and make decisions despite incomplete information.

Regarding consciousness and cognition, current AI systems lack true awareness and emotions. Their “decisions” are purely algorithmic outputs based on data, devoid of subjective experience or emotional involvement. Humans, on the other hand, not only process information but also possess consciousness, emotions, and subjective experiences, which are essential components of human intelligence.

In multitasking, while some AI systems can handle multiple tasks simultaneously, this often requires complex, targeted designs. Most AI systems are typically designed for single tasks, and their efficiency and effectiveness in multitasking typically do not match those of the human brain, which can quickly switch between tasks while maintaining high efficiency.

In terms of energy consumption and efficiency, advanced AI systems, especially large machine learning models, often demand significant computational resources and energy, far exceeding that of the human brain. The brain operates on about 20 watts, showcasing exceptionally high information processing efficiency.

Overall, while artificial intelligence has demonstrated remarkable performance in specific areas, it still cannot fully replicate the human brain, particularly in flexibility, learning efficiency, and multitasking. Future AI research may continue to narrow these gaps, but the complexity and efficiency of the human brain remain benchmarks that are difficult to surpass.

▷ Spooky Pooka ltd

1.3.2 Differences in Underlying Mechanisms

In terms of structure, modern AI systems, especially neural networks, are inspired by biological neural networks, yet the “neurons” (typically computational units) and their interconnections rely on numerical simulations. The connections and processing in these artificial neural networks are usually pre-set and static, lacking the dynamic plasticity of biological neural networks. The human brain comprises approximately 86 billion neurons, each connected to thousands to tens of thousands of other neurons via synapses [6-8], supporting complex parallel processing and highly dynamic information exchange.

Regarding signal transmission, AI systems transmit signals through numerical calculations. For instance, in neural networks, the output of a neuron is a function of the weighted sum of its inputs, processed using simple mathematical functions such as Sigmoid or ReLU. Neural signal transmission relies on electrochemical processes, where information exchange between neurons occurs through the release of neurotransmitters at synapses, regulated by various biochemical processes.

In terms of learning mechanisms, AI learning typically adjusts parameters (such as weights) through algorithms, such as backpropagation. Although this method is technically effective, it requires substantial amounts of data and necessitates retraining or significant adjustment of model parameters for new datasets, highlighting a gap compared to the brain’s continuous and unsupervised learning approach. Learning in the human brain relies on synaptic plasticity, where the strength of neural connections changes based on experience and activity, supporting ongoing learning and memory formation.

1.4 Background and Definition of the Long-Term Goal of Simulating Human Intelligence—Artificial General Intelligence

The concept of Artificial General Intelligence (AGI) arose from recognizing the limitations of narrow artificial intelligence (AI). Narrow AI typically focuses on solving specific, well-defined problems, such as board games or language translation, but lacks the flexibility to adapt across tasks and domains. As technology advances and our understanding of human intelligence deepens, scientists begin to envision an intelligent system with human-like cognitive abilities, self-awareness, creativity, and logical reasoning across multiple domains.

AGI aims to create an intelligent system capable of understanding and solving problems across various fields, with the ability to learn and adapt independently. This system would not merely serve as a tool; instead, it would participate as an intelligent entity in human socio-economic and cultural activities. The proposal of AGI represents the ideal state of AI development, aspiring to achieve and surpass human intelligence in comprehensiveness and flexibility.

 

2. Pathways to Achieving Artificial General Intelligence

Diverse neuron simulations and network structures exhibit varying levels of complexity. Neurons with richer dynamic descriptions possess higher internal complexity, while networks with wider and deeper connections exhibit greater external complexity. From the perspective of complexity, there are currently two promising pathways to achieve Artificial General Intelligence: one is the external complexity large model approach, which involves increasing the width and depth of the model; the other is the internal complexity small model approach, which entails adding ion channels to the model or transforming it into a multi-compartment model.

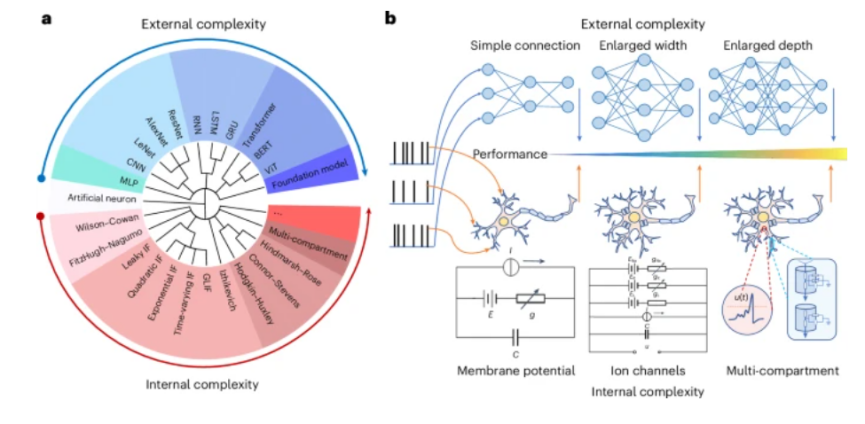
▷ Fig.3: Internal and external complexity of neurons and networks.

 

2.1 External Complexity Large Model Approach

In the field of artificial intelligence (AI), researchers increasingly rely on the development of large AI models to tackle broader and more complex problems. These models typically feature deeper, larger, and wider network structures, known as the “external complexity large model approach.” The core of this method lies in enhancing the model’s ability to process information (especially when dealing with large data sets) and learn by scaling up the model.

2.1.1 Applications of Large Language Models

Large language models, such as GPT (Generative Pre-trained Transformer) and BERT (Bidirectional Encoder Representations from Transformers), are currently hot topics in AI research. These models learn from vast text data using deep neural networks, master the deep semantics and structures of language, and demonstrate exceptional performance in various language processing tasks. For instance, GPT-3, trained on a massive text dataset, not only generates high-quality text but also performs tasks like question answering, summarization, and translation.

The primary applications of these large language models include natural language understanding, text generation, and sentiment analysis, making them widely applicable in fields such as search engines, social media analysis, and automated customer service.

2.1.2 Why Expand Model Scale?

According to research by Jason Wei, Yi Tay, William Fedus, and others in “Emergent Abilities of Large Language Models,” as the model size increases, a phenomenon of “emergence” occurs, where certain previously latent capabilities suddenly become apparent. This is due to the model’s ability to learn deeper patterns and associations by processing more complex and diverse information.

For example, ultra-large language models can exhibit problem-solving capabilities for complex reasoning tasks and creative writing without specific targeted training. This phenomenon of “emergent intelligence” suggests that by increasing model size, a broader cognitive and processing capability closer to human intelligence can be achieved.

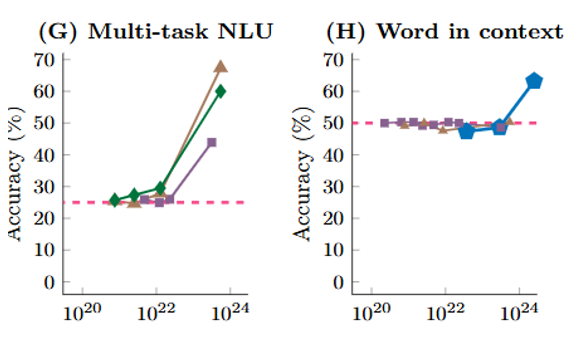
▷ Fig.4: The emergence of large language models.

2.1.3 Challenges

Despite the unprecedented capabilities brought by large models, they face significant challenges, particularly concerning efficiency and cost.

First, these models require substantial computational resources, including high-performance GPUs and extensive storage, which directly increases research and deployment costs. Second, the energy consumption of large models is increasingly concerning, affecting their sustainability and raising environmental issues. Additionally, training these models requires vast amounts of data input, which may lead to data privacy and security issues, especially when sensitive or personal information is involved. Finally, the complexity and opacity of large models may render their decision-making processes difficult to interpret, which could pose serious problems in fields like healthcare and law, where high transparency and interpretability are crucial.

2.2 Internal Complexity Small Model Approach

When discussing large language models, they leave a strong impression with their highly “human-like” output capabilities. Webb et al. examined the analogical reasoning abilities of ChatGPT [3] and found that it has emerged with zero-shot reasoning capabilities, enabling it to address a wide range of analogical reasoning problems without explicit training. Some believe that, if large language models (LLMs) like ChatGPT can indeed produce human-like responses to common psychological measures (such as judgments about actions, recognition of values, and views on social issues), they may eventually replace human subject groups in the future.

2.2.1 Theoretical Foundations

Neurons are the fundamental structural and functional units of the nervous system, primarily composed of cell bodies, axons, dendrites, and synapses. These components work together to receive, integrate, and transmit information. The following sections will introduce the theoretical foundations of neuron simulation, covering neuron models, the conduction of electrical signals in neuronal processes (dendrites and axons), synapses and synaptic plasticity models, and models with complex dendrites and ion channels.

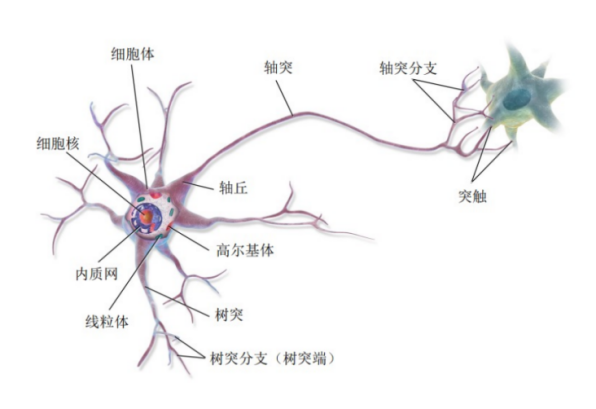
▷ Fig.5: Structure of a neuron.

 

(1) Neuron Models

Ion Channels

Ion channels and pumps in neurons are crucial membrane proteins that regulate the transmission of neural electrical signals. They control the movement of ions across the cell membrane, thereby influencing the electrical activity and signal transmission of neurons. These structures ensure that neurons can maintain resting potentials and generate action potentials, forming the foundation of the nervous system’s function.

Ion channels are protein channels embedded in the cell membrane that regulate the passage of specific ions (such as sodium, potassium, calcium, and chloride). Various factors, including voltage changes, chemical signals, and mechanical stress, control the opening and closing of these ion channels, impacting the electrical activity of neurons.

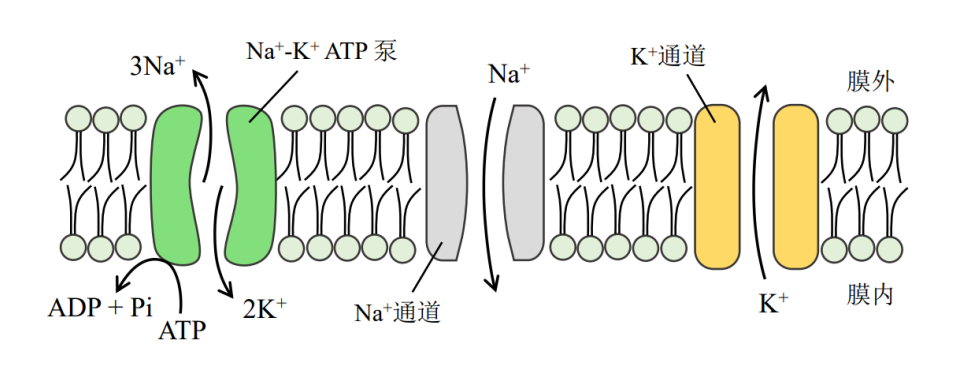
▷ Fig.6: Ion channels and ion pumps for neurons.

Equivalent Circuit

The equivalent circuit model simulates the electrophysiological properties of neuronal membranes using circuit components, allowing complex biological electrical phenomena to be explained and analyzed within the framework of physics and engineering. This model typically includes three basic components: membrane capacitance, membrane resistance, and a power source.

The cell membrane of a neuron exhibits capacitive properties related to its phospholipid bilayer structure. The hydrophobic core of the lipid bilayer prevents the free passage of ions, resulting in high electrical insulation of the cell membrane. When the ion concentrations differ on either side of the cell membrane, especially under the regulation of ion pumps, charge separation occurs. Due to the insulating properties of the cell membrane, this charge separation creates an electric field that allows the membrane to store charge.

Capacitance elements are used to simulate this charge storage capability, with capacitance values depending on the membrane’s area and thickness. Membrane resistance is primarily regulated by the opening and closing of ion channels, directly affecting the rate of change of membrane potential and the cell’s response to current input. The power source represents the electrochemical potential difference caused by the ion concentration gradient across the membrane, which drives the maintenance of resting potential and the changes in action potential.

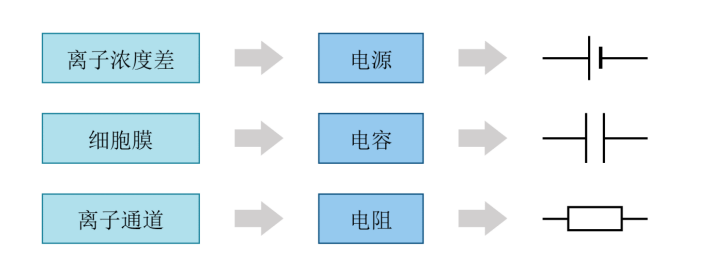
▷ Fig.7: Schematic diagram of the equivalent circuit.

Hodgkin-Huxley Model

Based on the idea of equivalent circuits, Alan Hodgkin and Andrew Huxley proposed the Hodgkin-Huxley (HH) model in the 1950s based on their experimental research on the giant axon of the squid. This model includes conductances for sodium (Na), potassium (K), and leak currents, representing the opening degree of each ion channel. The opening and closing of the ion channels in the model are further described by gating variables, which are voltage- and time-dependent (m, h, n). The equations of the HH model are as follows:

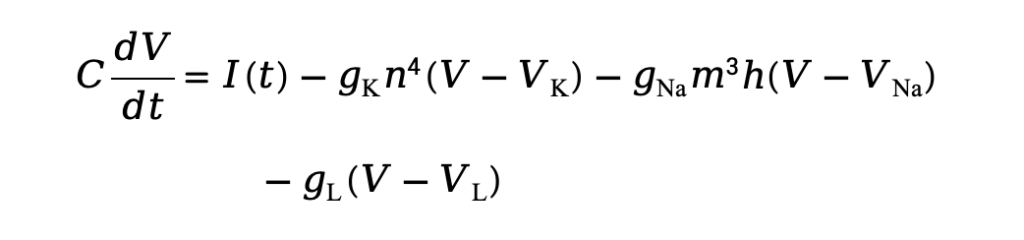
Where is the membrane potential, is the input current, ​, ​, and are the maximum conductances for potassium, sodium, and leak currents, respectively. ​, ​, and ​ are the equilibrium potentials for potassium, sodium, and leak currents, respectively. , and are variables associated with the states of ion channel gating for potassium and sodium currents.
The dynamics can be described by the following differential equations:

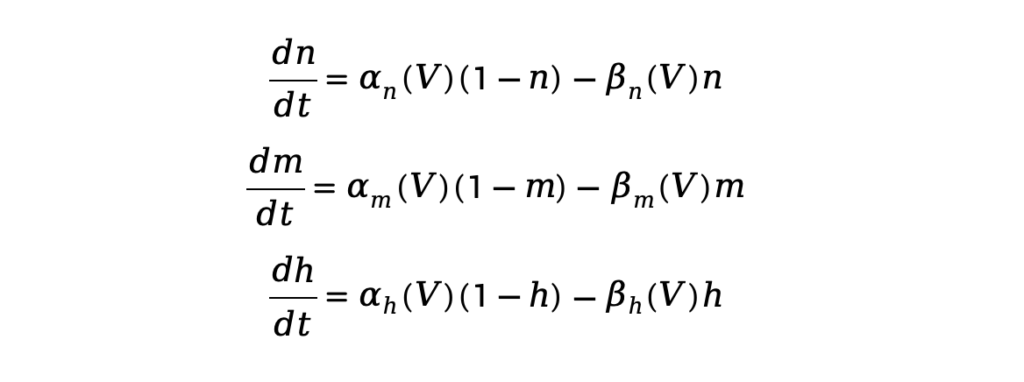
The and functions represent the rates of channel opening and closing, which were experimentally determined using the patch-clamp technique.

Leaky Integrate-and-Fire Model (LIF)

The Leaky Integrate-and-Fire model (LIF) is a commonly used mathematical model in neuroscience that simplifies the action potential of neurons. This model focuses on describing the temporal changes in membrane potential [4-5] while neglecting the complex ionic dynamics within biological neurons.

Scientists have found that when a continuous current input is applied to a neuron [6-7], the membrane potential rises until it reaches a certain threshold, leading to the firing of an action potential, after which the membrane potential rapidly resets and the process repeats. Although the LIF model does not describe the specific dynamics of ion channels, its high computational efficiency has led to its widespread application in neural network modeling and theoretical neuroscience research. Its basic equation is as follows:

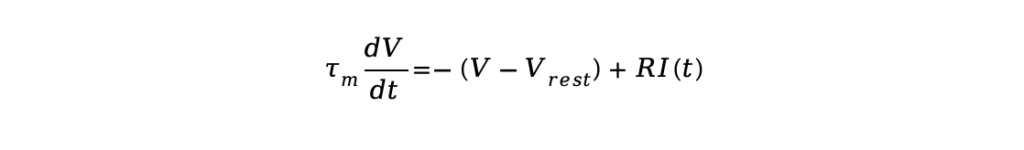
Where is the membrane potential; is the resting membrane potential; is the input current; is the membrane resistance; and is the membrane time constant, reflecting the rate at which the membrane potential responds to input current. is the membrane capacitance.

In this model, when the membrane potential reaches a specific threshold value ​, the neuron fires an action potential (spike). Subsequently, the membrane potential is reset to a lower value ​ to simulate the actual process of neuronal firing.

(2) Conduction of Electrical Signals in Neuronal Processes (Cable Theory)

In the late 19th to early 20th centuries, scientists began to recognize that electrical signals in neurons could propagate through elongated neural fibers such as axons and dendrites. However, as the distance increases, signals tend to attenuate. Researchers needed a theoretical tool to explain the propagation of electrical signals in neural fibers, particularly the voltage changes over long distances.

In 1907, physicist Wilhelm Hermann proposed a simple theoretical framework that likened nerve fibers to cables to describe the diffusion process of electrical signals. This theory was later further developed in the mid-20th century by Hodgkin, Huxley, and others, who confirmed the critical role of ion flow in signal propagation through experimental measurements of neurons and established mathematical models related to cable theory.

The core idea of cable theory is to treat nerve fibers as segments of a cable, introducing electrical parameters such as resistance and capacitance to simulate the propagation of electrical signals (typically action potentials) within nerve fibers. Nerve fibers, such as axons and dendrites, are viewed as one-dimensional cables, with electrical signals propagating along the length of the fiber; membrane electrical activity is described through resistance and capacitance, with current conduction influenced by internal resistance and membrane leakage resistance; the signal gradually attenuates as it propagates through the fiber.

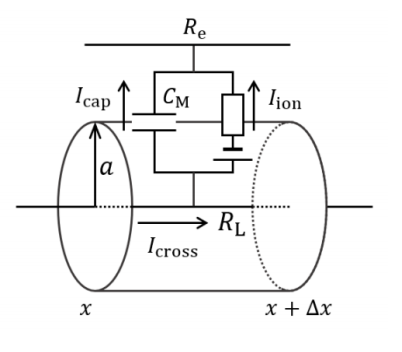
▷ Fig.8: Schematic diagram of cable theory.

The cable equation is:

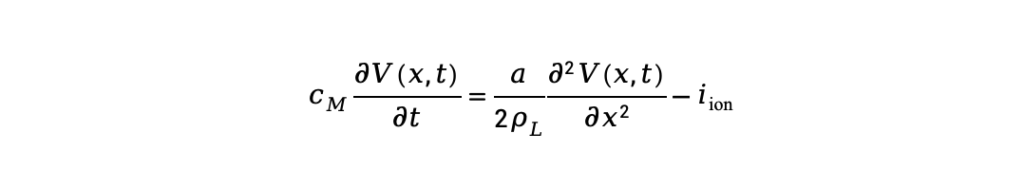
Where ​ represents the membrane capacitance per unit area, reflecting the role of the neuronal membrane as a capacitor; is the radius of the nerve fiber, which affects the propagation range of the electrical signal; ​ is the resistivity of the nerve fiber’s axial cytoplasm, describing the ease of current propagation along the fiber; and ​ is the ionic current density, representing the flow of ion currents through the membrane.

The temporal change, governed by the term CM and ∂ V(x,t) / ∂ t​, reflects how the membrane potential changes over time; the spatial spread, represented by the term (α/ 2 ρL)*(∂^2 V(x,t)/ ∂^2 x*2), describes the gradual spread and attenuation of the signal along the nerve fiber, which is related to the fiber’s resistance and geometry. The term​ iion indicates the ionic current through the membrane, which controls the generation and recovery of the action potential. The opening of ion channels is fundamental to signal propagation.

 

(3) Multi-Compartment Model

In earlier neuron modeling, such as the HH model and cable theory, neurons were simplified to a point-like “single compartment,” only considering temporal changes in membrane potential while neglecting the spatial distribution of various parts of the neuron. These models are suitable for describing the mechanisms of action potential generation but fail to fully explain signal propagation in the complex morphological structures of neurons (such as dendrites and axons).

As neuroscience deepened its understanding of the complexity of neuronal structures, scientists recognized that voltage changes in different parts of the neuron can vary significantly, especially in neurons with long dendrites. Signal propagation in dendrites and axons is influenced not only by the spatial diffusion of electrical signals but also by structural complexity, resulting in different responses. Thus, a more refined model was needed to describe the spatial propagation of electrical signals in neurons, leading to the development of the multi-compartment model.

The core idea of the multi-compartment model is to divide the neuron’s dendrites, axons, and cell body into multiple interconnected compartments, with each compartment described using equations similar to those of cable theory to model the changes in transmembrane potential  over time and space. By connecting multiple compartments, the model simulates the complex propagation pathways of electrical signals within neurons and reflects the voltage differences between different compartments. This approach allows for precise description of electrical signal propagation in the complex morphology of neurons, particularly the attenuation and amplification of electrical signals on dendrites.

Specifically, neurons are divided into multiple compartments, each representing a portion of the neuron (such as dendrites, axons, or a segment of the cell body). Each compartment is represented by a circuit model, with resistance and capacitance used to describe the electrical properties of the membrane. The transmembrane potential is determined by factors such as current injection, diffusion, and leakage. Adjacent compartments are connected by resistors, and electrical signals propagate between compartments through these connections. The transmembrane potential Vi follows a differential equation similar to cable theory in the i-th compartment:

Where Ci is the membrane capacitance of compartment, Imem,i(t) is the membrane current, and Raxial,i is the axial resistance between compartments. These coupled equations describe how the signal propagates and attenuates within different compartments of the neuron.

In the multi-compartment model, certain compartments (such as the cell body or initial segment) can generate action potentials, while others (like dendrites or axons) primarily facilitate the propagation and attenuation of electrical signals. Signals are transmitted through connections between different compartments, with input signals in the dendritic region ultimately integrated at the cell body to trigger action potentials, which then propagate along the axon.

Compared to single-compartment models, the multi-compartment model can better reflect the complexity of neuronal morphological structures, particularly in the propagation of electrical signals within structures like dendrites and axons. Due to the coupling differential equations involving multiple compartments, the multi-compartment model often requires numerical methods (such as the Euler method or Runge-Kutta method) for solution.

2.2.2 Why Conduct Complex Dynamic Simulations of Biological Neurons?

Research by Beniaguev et al. has shown that the complex dendritic structures and ion channels of different types of neurons in the brain enable a single neuron to possess extraordinary computational capabilities, comparable to those of a 5-8 layer deep learning network [8].

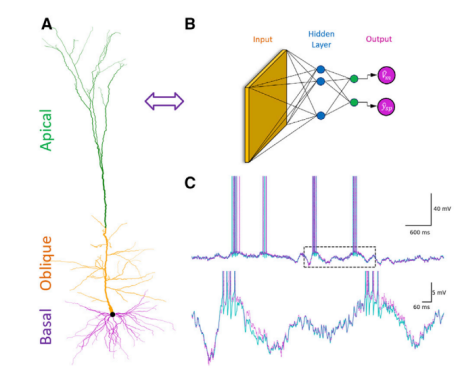
▷ Fig.9: A model of Layer 5 cortical pyramidal neurons with AMPA and NMDA synapses, accurately simulated using a Time Convolutional Network (TCN) with seven hidden layers, each containing 128 feature maps, and a historical duration of 153 milliseconds.

He et al. focused on the relationships between different internal dynamics and complexities of neuron models [9]. They proposed a method for converting external complexity into internal complexity, noting that models with richer internal dynamics exhibit certain computational advantages. Specifically, they theoretically demonstrated the equivalence of dynamic characteristics between the LIF model and the HH model, showing that an HH neuron can be dynamically equivalent to four time-varying parameter LIF neurons (tv-LIF) with specific connection structures.

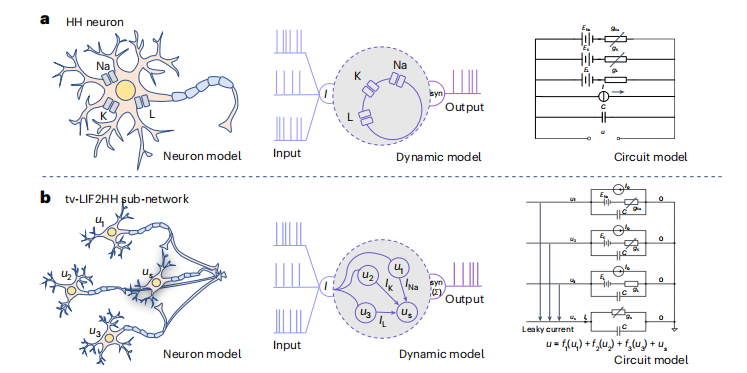
▷ Fig.10: A method for converting from the tv-LIF model to the HH model.

Building on this, they experimentally validated the effectiveness and reliability of HH networks in handling complex tasks. They discovered that the computational efficiency of HH networks is significantly higher compared to simplified tv-LIF networks (s-LIF2HH). This finding demonstrates that converting external complexity into internal complexity can enhance the computational efficiency of deep learning models. It suggests that the internal complexity small model approach, inspired by the complex dynamics of biological neurons, holds promise for achieving more powerful and efficient AI systems.

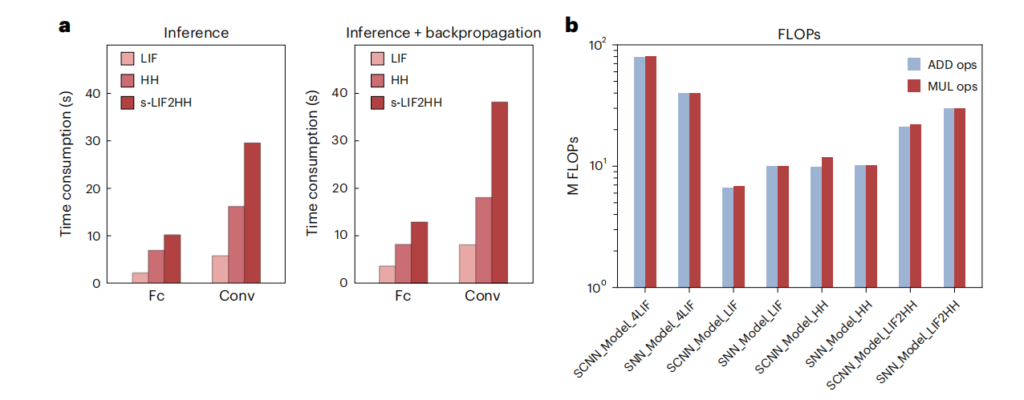
▷ Fig.11: Computational resource analysis of the LIF model, HH model, and s-LIF2HH.

Moreover, due to structural and computational mechanism limitations, existing artificial neural networks differ greatly from real brains, making them unsuitable for directly understanding the mechanisms of real brain learning and perception tasks. Compared to artificial neural networks, neuron models with rich internal dynamics are closer to biological reality. They play a crucial role in understanding the learning processes of real brains and the mechanisms of human intelligence.

2.3 Challenges

Despite the impressive performance of the internal complexity small model approach, it faces a series of challenges. The electrophysiological activity of neurons is often described by complex nonlinear differential equations, making model analysis and solution quite challenging. Due to the nonlinear and discontinuous characteristics of neuron models, using traditional gradient descent methods for learning becomes complex and inefficient. Furthermore, increasing internal complexity, as seen in models like HH, reduces hardware parallelism and slows down information processing speed. This necessitates corresponding innovations and improvements in hardware.

To tackle these challenges, researchers have developed various improved learning algorithms. For example, approximate gradients are used to address discontinuous characteristics, while second-order optimization algorithms capture curvature information of the loss function more accurately to accelerate convergence. The introduction of distributed learning and parallel computing allows the training process of complex neuron networks to be conducted more efficiently on large-scale computational resources.

Additionally, bio-inspired learning mechanisms have garnered interest from some scholars. The learning processes of biological neurons differ significantly from current deep learning methods. For instance, biological neurons rely on synaptic plasticity for learning, which includes the strengthening and weakening of synaptic connections, known as long-term potentiation (LTP) and long-term depression (LTD). This mechanism is not only more efficient but also reduces the model’s dependence on continuous signal processing, thereby lowering the computational burden.

▷ MJ

3. Bridging the Gap Between Artificial Intelligence and Human Brain Intelligence

He et al. theoretically validated and simulated that smaller, internally complex networks can replicate the functions of larger, simpler networks. This approach not only maintains performance but also enhances computational efficiency, reducing memory usage by four times and doubling processing speed. This suggests that increasing internal complexity may be an effective way to improve AI performance and efficiency.

Zhu and Eshraghian commented on He et al.’s article, “Network Model with Internal Complexity Bridges Artificial Intelligence and Neuroscience” [5]. They noted, “The debate over internal and external complexity in AI remains unresolved, with both approaches likely to play a role in future advancements. By re-examining and deepening the connections between neuroscience and AI, we may discover new methods for constructing more efficient, powerful, and brain-like artificial intelligence systems.”

As we stand at the crossroads of AI development, the field faces a critical question: Can we achieve the next leap in AI capabilities by more precisely simulating the dynamics of biological neurons, or will we continue to advance with larger models and more powerful hardware? Zhu and Eshraghian suggest that the answer may lie in integrating both approaches, which will continuously optimize as our understanding of neuroscience deepens.

Although the introduction of biological neuron dynamics has enhanced AI capabilities to some extent, we are still far from achieving the technological level required to simulate human consciousness. First, the completeness of the theory remains insufficient. Our understanding of the nature of consciousness is lacking, and we have yet to develop a comprehensive theory capable of explaining and predicting conscious phenomena. Second, simulating consciousness may require high-performance computational frameworks that current hardware and algorithm efficiencies cannot yet support. Moreover, efficient training algorithms for brain models remain a challenge. The nonlinear behavior of complex neurons complicates model training, necessitating new optimization methods. Many complex brain functions, such as long-term memory retention, emotional processing, and creativity, still require in-depth exploration of their specific neural and molecular mechanisms. How to further simulate these behaviors and their molecular mechanisms in artificial neural networks remains an open question. Future research must make breakthroughs on these issues to truly advance the simulation of human consciousness and intelligence.

Interdisciplinary collaboration is crucial for simulating human consciousness and intelligence. Cooperative research across mathematics, neuroscience, cognitive science, philosophy, and computer science will deepen our understanding and simulation of human consciousness and intelligence. Only through collaboration among different disciplines can we form a more comprehensive theoretical framework and advance this highly challenging task.